1tan2θ=sec2θ 1 tan 2 θ = sec 2 θ The second and third identities can be obtained by manipulating the first The identity 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θ is found by rewriting the left side of the equation in terms of sine and cosine Prove 1cot2θ = csc2θ 1 cot 2 θ = csc 2 θThe Pythagorean identity sin^2(x)cos^2(x)= 1 is useful in proving the identity tan(x)sec(x)= (cos(x)/(1sin(x))) true or false Answer by stanbon(757) ( Show Source )Question 32 SURVEY 900 seconds Q Use a doubleangle or halfangle identity to find the exact value of each expression cos θ = 4/5 and 270° < θ < 360°Find sin 2θ answer choices 1/5 24/25

Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube
Tan 2x sec 2x 1 true or false
Tan 2x sec 2x 1 true or false-Answer and Explanation 1 We are given the equation tan2(x)1 = sec2(x) tan 2 ( x) 1 = sec 2 ( x) The given equation is true since it is one of the Pythagorean identities inTranscribed image text 1 Multiply and simplify cos2x(1 tan²x) = 2 True or false?




Solved Enter T Or F Depending On Whether The Statement Is Chegg Com
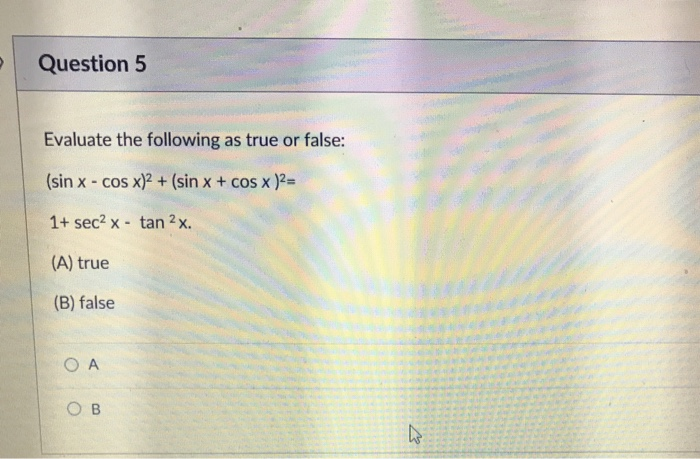
Justify your answer 2 ( points) Find ∫ 0 π 4 sec 2 θ tan 2 θ 1 d θ 3 ( points) Show that ∫ 0 π 2 sin 2 x d x = ∫ 0 π 2 cos 2 x d x 4 ( points) Find the indefinite integral ∫ ( sin 3 x ) ( c o s x ) d x Question Chapter 4 Discussion 1 ( points) True or False? sin^2 (x) cos^2 (x) = 1 everywhere An alternate approach to proving this identity involves using the "unit circle" (radius = 1) Since the radius isCos (x) sin (x) = cos x sin x 3 Prove tan x sin x = sec XCOS X 4 Write as one trigonometric function using an identity sin 42° cos 35° cos 42° sin 35° 5 Use a sum or difference identity and the unit circle to evaluate sin (199) 12 exactly 6
The equation sec^2x1=tan^2 x is an identity True or false?Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!True or False On the scan form A = true and B = false (1 pt each) 1 Given x > 0, d dx tan x = sec2 x 2 Given y > 0, tan y = sec2 y 3 ln e = 0 4 log 7 x = 1 x 5 The derivative of f(x) = 7x is f ' (x) = (x)7 x1 6 cos1 x is equal to 2 1 1x 7 The derivative of f(x) = csc 2x is f ' (x) = – csc 2x cot 2x 8 The derivative of f(x
250 TOP MCQs on Derivatives & Answers Class 11 Maths Mathematics Multiple Choice Questions on "Derivatives" 1 Find the derivative of e x2 a) e x2 b) 2xTan 1 p tan 2 1 sec2 d = Z tan 1 p sec sec2 d Remember to think carefully about the p sec2 part From here we can proceed as normal (assuming sec is positive, just for simplicity) = Z tan 1 sec sec2 d = Z tan sec sec d And we've successfully reduced the problem to an integral we can do Ivan Khatchatourian MAT137 1 February, 18 7 / 31 tan2x sec2x = 1 So, the original statement is false Sure, there might be values of x for which the original equation works It's solvable, but that doesn't make it true for all x When you started messing with the equation by rewriting it as sines and cosines, I think you goofed the math sin2x/cos2x 1/cos2x = 1




How Do You Simplify Sec 4x Tan 4x Sec 2x Tan 2x Socratic




Answered 1 True Or False T F L Cosx Sec X Bartleby
Chapter 5 True Or False and Multiple Choice Problems 1 For each of the following ten statements answer TRUE or FALSE as appropriate (a) If f is di↵erentiable on 1,1 then f The equation tan^2 x1=sec^2 x is an identity true or falseTrigonometric Identities Solver \square!



1 Tan 2x Sec 2x




Search Results For Page 38 Samacheer Kalvi
Write the converse and decide whether the converse is true or false (iii) If x^2=1 , then x=1True or false the equation tan^2x1=sec^2xNone ANSWERTrueEXPLANATIONThe given trigonometric equation is We take the LHS and simplify to arrive at the RHS Collect LCM on the right hand side to get;Justify your conclusion with a counterexample or a proof For each integer n, if n is odd, then 8 j(n2 1) The statement is true If n is an odd integer, then there exists k 2Z such that n = 2k 1 Then, n2 1 = (2k 1)2 1 = 4k2 4k = 4k(k 1) Notice that k and k 1 are consecutive integers
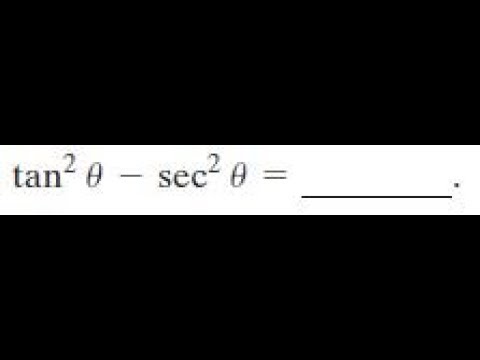



Tan 2x Sec 2x Youtube



2
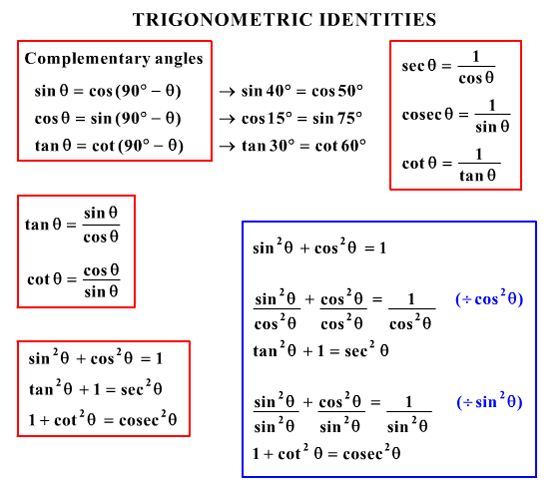
The Trigonometric Identities are equations that are true for Right Angled Triangles Periodicity of trig functions Sine, cosine, secant, and cosecant have period 2π while tangent and cotangent have period π Identities for negative angles Sine, tangent, cotangent, and cosecant are odd functions while cosine and secant are even functions #2 tan x/(1tan^2x)=(2sin x/cos x)/(1(sin^2x/cos^2x)# #=2 sin x cos x/(cos^2xsin^2x)# #=(sin 2x)/(cos 2x)=tan 2x# Proofs for #sin 2x = 2 sin x cos x and cos 2x = 1 2 sin^2x# Use Area of a #triangle# ABC = 1/2(base)(altitude) = 1/2 bc sin A Here, it is the #triangle# ABC of a unit circle, with center at A, B and C on the circle and #angle# A = 2x Here, AB = AC = 1, BC =7 Is the following proposition true of false?




Sec 6x Tan 6x 1 2 Tan 2x Sec 2x Important Difficult Trigonometric Identity Youtube
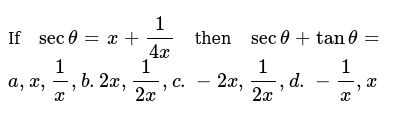



The Equation Sec 2x 1 Tan 2x Is An Identity True Or False
View Practice Test 61 (7)pdf from MATH MISC at American Military University WEEK 11 ANALYTIC TRIGONOMETRY PART 1 SECTIONS 61 62 61 Fundamental Trigonometric Identities PRACTICE TESTClick here👆to get an answer to your question ️ If 2tan^2x 5sec x = 1 for exactly seven distinct values of x epsilon 0, npi2 , n epsilon N , then find the greatest value of n 2 tan 2 x − 5 sec x = 1 2 State whether the following statement is true or false Justify your answer sec A = 5 1 21 See answer bailee10 is waiting for your help Add your answer and earn points




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo
1 True or False, and explain (a) The derivative of a polynomial is a polynomial False The notation, sec−1(x) is for the inverse secant function, which is not the reciprocal of the secant (d) d dx (10 x) = x10x−1 False xex2(x2 1)10 1 2x 2x x x2 1 (j)Trigonometric Simplification Calculator \square!Tan 1(2x) dx= xtan 1(2x) 1 4 lnj1 4x2j Cusing IBP R e 1 x3x1 x dx= (e3 1)=3 eby dividing rst and ln(e) = 1, etc lim n!1cos(2ˇn) = 1 because cos(2ˇn) = cos(0) = 1 P 1 k=1 (1 2 1 3) = 1 3, telescoping (write out a few terms) R tan3(2x)sec(2x) dx= sec 3(2x) 6 sec(2x) 2 Cusing u= sec(2x




How Do You Prove Tan 2x Secx 1 1 Secx Socratic



True Or False And Multiple Choice Problems
Adal2762 adal2762 Mathematics Middle School answered True or false the equation tan^2x1=sec^2x 1 See answer Advertisement Advertisement adal2762 is waiting for your help Add your answer and earn pointsChapter 5 True Or False and Multiple Choice Problems 🔗 Answer the following questions For each of the following ten statements answer TRUE or FALSE as appropriate If f f is differentiable on −1,1 − 1, 1 then f f is continuous at x= 0 x = 0 If f′(x)< 0 f ′ ( x) < 0 and f "(x)> 0 f " ( x) > 0 for all x x then f f is concaveGet the answers you need, now!




How Do You Solve 1 Tan 2x 6 2sec 2x Socratic




Integrating Using Different Methods 60 Questions Teaching Resources
(tan x csc 2 x tan x sec 2 x) (1 tan x 1 cot x) For the following exercises, determine whether the identity is true or false If false, find an appropriate equivalent expression 40Sec^(1)((1tan^(2)x)/(1tan^(2)x)) Write the set of values of x for which 2 tan^(1)x=tan^(1)(2x)/(1x^(2)) holds Determine whether the inequality is TRUE or FALSE ((x 1)/(x))^(2) > (x 1 Free PDF Download of CBSE Maths Multiple Choice Questions for Class 12 with Answers Chapter 2 Inverse Trigonometric Functions Maths MCQs for Class 12 Chapter Wise with Answers PDF Download was Prepared Based on Latest Exam Pattern Students can solve NCERT Class 12 Maths Inverse Trigonometric Functions MCQs Pdf with Answers to know their




Solution 3 Sec Maths Studypool




Tan 2x Formula What Is Tan 2x Formula Examples
State whether the following are true or false Justify your answer (i) The value of tan A is always less than 1 (ii) sec A = 5 1 2 for some value of angle A (iii) cos A is the abbreviation used for the cosecant of angle A (iv) cot A is the product of cot and A (v) sin θ = 3 4 for some angle θ RD Sharma Class 10 Solutions Chapter 11 Trigonometric Identities MCQS Answer each of the following questions either in one word or one sentence or as per requirement of the questions Question 1 Define an identity Solution An identity is an equation which is true for all values of the variable (s) involvedGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



Question 5 Evaluate The Following As True Or False Chegg Com
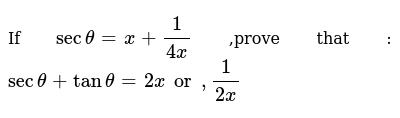



The Equation Sec 2x 1 Tan 2x Is An Identity True Or False
True or false the equation tan^2x1=sec^2x Get the answers you need, now!Bailee10 bailee10 Mathematics High School answered The equation sec^2x1=tan^2 x is an identity True or false? Application of Derivatives Class 12 Maths MCQs Pdf 1 The total revenue in ₹ received from the sale of x units of an article is given by R (x) = 3x² 36x 5 The marginal revenue when x = 15 is (in ₹ ) (a) 126 (b) 116




Verifying A Trigonometric Identity Tan 2 X 1 Sec X Sec X Youtube



Bestmaths Online Proof 4
1 p x (4)True or false and explain your answer There is at least one point xbetween 0 and 1 iv) ((x2 1)tan(x) 2x)sec(x) v) 15x2 4x vi) 1 (x 23)2(x 2) vii) 5 2x (x 2)2(x 3) 2 viii) 6 (x 2)2(x 3) ix) Not found x) 2xcos(x) x2 cos(x) cos2(x) xi) 2x (x1)2 xii) cos2(x) (8)Suppose g(x), h(x), and j(x) are di erentiable function with theFalse Take \(f(x)=1\) and \(g(x)=2\text{}\) True False Apply the Mean Value Theorem False Apply the chain rule False False True True The limit equals \(g'(2)\text{}\) False True \(\tan ^2x\sec ^2 x=1\text{}\) False \(\ds y=x^2x\) is not differentiable for all real numbers False False False Take \(\ds \lim _{x\to 5}\frac{x5}{x5}\text{}\) FalseX 7 e x dx = sec(x) tan(x) dx = 2 x x 2 1 dx = 12 t 3 t 3 dt = 2) (15 pts) More e 5 x dx = cos 2 (x) dx = tan 2 (x) dx = 3) (15 pts) A rancher has 0 feet of fencing with which to enclose two adjacent rectangular corrals (I drew a




Calculus Formula Definition Examples What Is Calculus




Integrate Sec 2x Method 1
This implies that This identity has been verified Therefore the correct answer is true(true or false) One disadvantage of polar equations is that you can use a polar function to describe a graph whose equation in rectangular coordinates would not be considered a function y=tan(2(x(pi )/(6))) If triangle ABC has angle 52 side a=0 and side b=234 then which of the following is true b=672 or 1128 tan^2xsec^2x=1 (trueFor each expression in column I, choose the expression from column II to complete an identity Column I Column II 1 tanxcosx A sin^2x/cos^2x 2 sec^2x1 B 1/sec^2x 3 sec x/cscx C sin(x) 4 1sin^2x Dcsc^2xcot^2xsin^2x 5 cos^2 x E tanx I figured PRE CALC
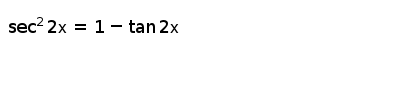



Tan 2x Sec 2x 1 For All Values Of X True Or False




Determine Whether Trigonometry Functions Are Linearly Independent Problems In Mathematics
(tan x csc 2 x tan x sec 2 x) (1 tan x 1 cot x) For the following exercises, determine whether the identity is true or false If false, find an appropriate equivalent expression 40Sin(2X) = 2 sinX cosX cos(2X) = 1 2sin 2 X = 2cos 2 X 1 tan(2X) = 2tanX / 1 tan 2 X Multiple Angle Formulas sin(3X) = 3sinX 4sin 3 X cos(3X) = 4cos 3 X 3cosX sin(4X) = 4sinXcosX 8sin 3 XcosX cos(4X) = 8cos 4 X 8cos 2 X 1 Half Angle Formulas The sides of the Eq'n are not sentences If you take either side's formula and show that it is equal to some other formula, without any unsupported or unwarranted assumptions, then you are logical Eg The RHS is always equal to $44/(2 \cos^2 x)=44/(1\cos 2 x)=4\cos 2 x/(1\cos 2 x)$ regardless of what is written on the LHS $\endgroup$




The Derivative Of Sec2x Derivativeit




Mathematics Question Of The Day With Solution Facebook
Tan^2 (2x) 1cos (6x)= 2sin^2 (3x) (true or false) sin (75 degrees)=sqrt (1cos (150 degrees)/2) true (TRUE or FALSE) The horizontal distance, in feet, traveled by a projectile can be modeled by the equation h = ( (v0^2)/16) sinθcosθ where θ is the initial angle and v0 is the initial velocityMAC 2311 Final Exam A recent topics and Key Prof S Hudson 1) ( pts) Compute and simplify;30 seconds Q Organize this equation so it can be factored 1−sin 2 x sinx = 1 answer choices move all to the right 0 = sin 2 x − sinx cancel the ones and cancel a sinx replace sin 2 x with 1 − cos 2 x use this 0 = sin 2 x − sinx 2



2



2
3 Answers tan^2 (x) sec^2 (x) = 1 LHS = 1/cos^2 (x) sin^2 (x)/cos^2 (x) = (1 sin^2 (x))/cos^2 (x) = cos^2 (x)/cos^2 (x) = 1 = RHS rhs = sec2x tan2x = (a million/ cos2x) (sin2x/cos 2x) = ( a million sin 2x) / cos 2x a million sin2x = a million 2sinx cosx = cos^ 2 x sin^2 x 2 sin x cosx ( as cos^ 2 x sin^2 x = a millionFind the second order derivatives of the following e2x tan x Mathematics and StatisticsFor the following problems, consider radioactive dating A human skeleton is found in an archeological dig Carbon dating is implemented to determine how old the skeleton is by using the equation latexy=e^{rt}/latex, where latexy/latex is the percentage of radiocarbon still present in the material, latext/latex is the number of years passed, and latexr=/latex is




Find The General Solution For Each Of The Following Equations Sec2 2x 1 Tan 2x Mathematics Shaalaa Com



True Or False The Equation Sec 2 X 1 Tan 2 X Is An Identity Brainly Com
Verify the identity tan x/sec x1=sec x1/tan x Verify cos(360 degreesx)=cos x Solve 4cos^3x3cosx=0 for 0 less than or equal to xVerify that the equation is an identity, dfrac{cos x}{sec x} dfrac{sin x}{csc x} = sec^2 x tan^2 x Show your work View Answer Prove the identity tanxsin2x = 2 2cos^{2}x




Integral 1 Tan 2 X Sec 2 X Youtube



1




Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby




Tan 2x Sec 2x 1 For All Values Of X True Or False Brainly Com




State Whether The Following Are True Or False Justify Your Answer I Sin A B Sina Sinb Ii The Value Of Sintheta Increases As Theta Increases Iii The Value Of Costheta



Kbqwrl1sumsuwm



Solved Consider The Possible Identity Tan 2x Cos 2x 1 Cos 2x Sec 2x A State Any Non Permissible Values B Attempt To Verify Possible Identity Course Hero




Match The Corresponding Trigonometric Expressions Gauthmath



Find The General Solution For The Equation Sec 2 2x 1 Tan 2x Sarthaks Econnect Largest Online Education Community



Verify Tan 2x Sec 2x Brainly Com



Is This Correct Because My Book Says The Answer Is Tan 2x Sec 2x Secx Calculus



Tan 2x Sec 2x 1 Sec 2x Tan 2x 1 10 12 2 Sarthaks Econnect Largest Online Education Community



True Or False And Multiple Choice Problems
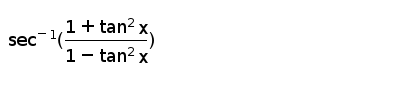



The Equation Sec 2x 1 Tan 2x Is An Identity True Or False



Solved Find The Derivative Using Inverse Trigonometric Functions And Simplify Further If Possible Course Hero




Sec 2 2x 1 Tan2x Youtube




How To Use Algebra Tiles To Model Solve Equations Video Lesson Transcript Study Com
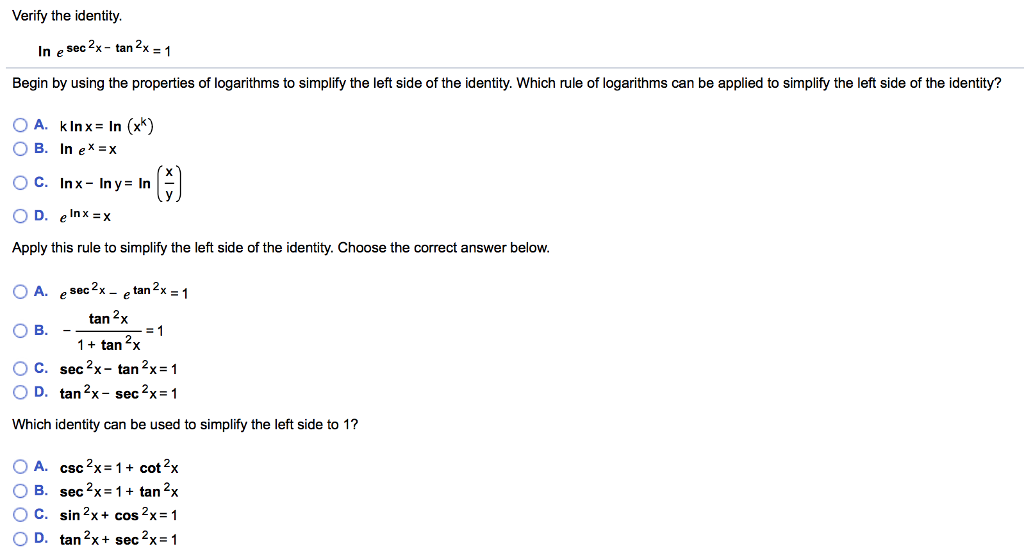



Solved Verify The Identity In Esec 2x Tan 2x 1 Begin By Chegg Com



Arxiv Org




Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified




Powers Of Trigonometric Functions




Bhasvic Maths 1 A1 Doubles Assignment 12a Ppt Download
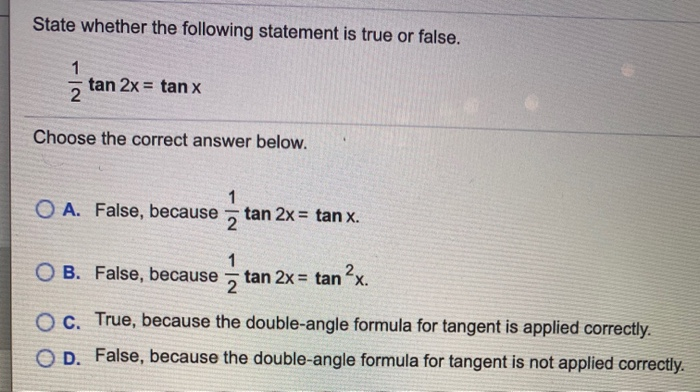



Solved State Whether The Following Statement Is True Or Chegg Com



Engineered Yeast Genomes Accurately Assembled From Pure And Mixed Samples Nature Communications




How Do You Prove Tan 2x Secx 1 1 Secx Socratic



E Frac Cos 2x1 Sin 2x Sec 2x Tan 2x Prove Gauthmath
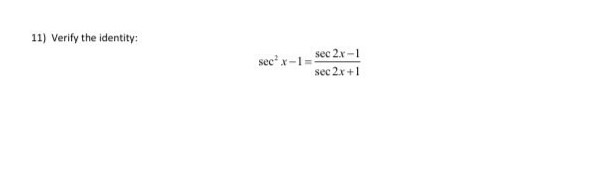



Answered 11 Verify The Identity Sec 2x 1 Sec Bartleby




The Equation Sec 2x 1 Tan 2x Is An Identity True Or False Brainly Com
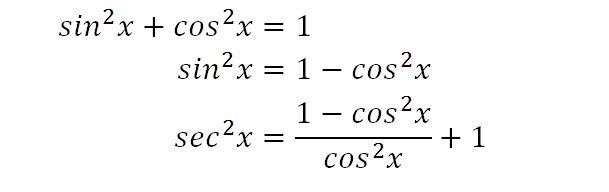



Integrate Sec 2x Method 2
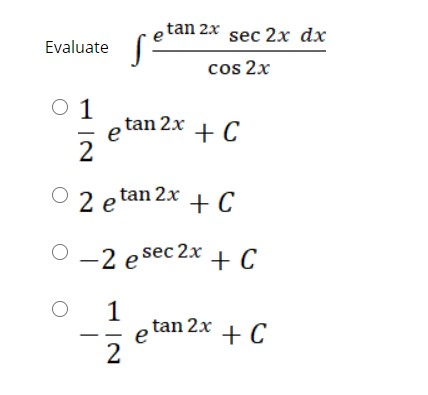



Answered Tan 2x Sec 2x Dx Evaluate Cos 2x O 1 Bartleby




How Do You Integrate 1 Tan2x Sec2x Dx Socratic



2




How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic




Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3



1




Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube




Answers To Review Problems For Calculus I Past Final Exam Math 1210 Docsity




Tan 2x Sec 2x 1 True Or False For All Values Of X Wyzant Ask An Expert




Integrate Sec 2x Method 2



What Would Be Steps In Proving That Tan2x Secx 1 1 Sec X Socratic



How Do We Prove That Tan2x 1 Sec2x Tanx Quora
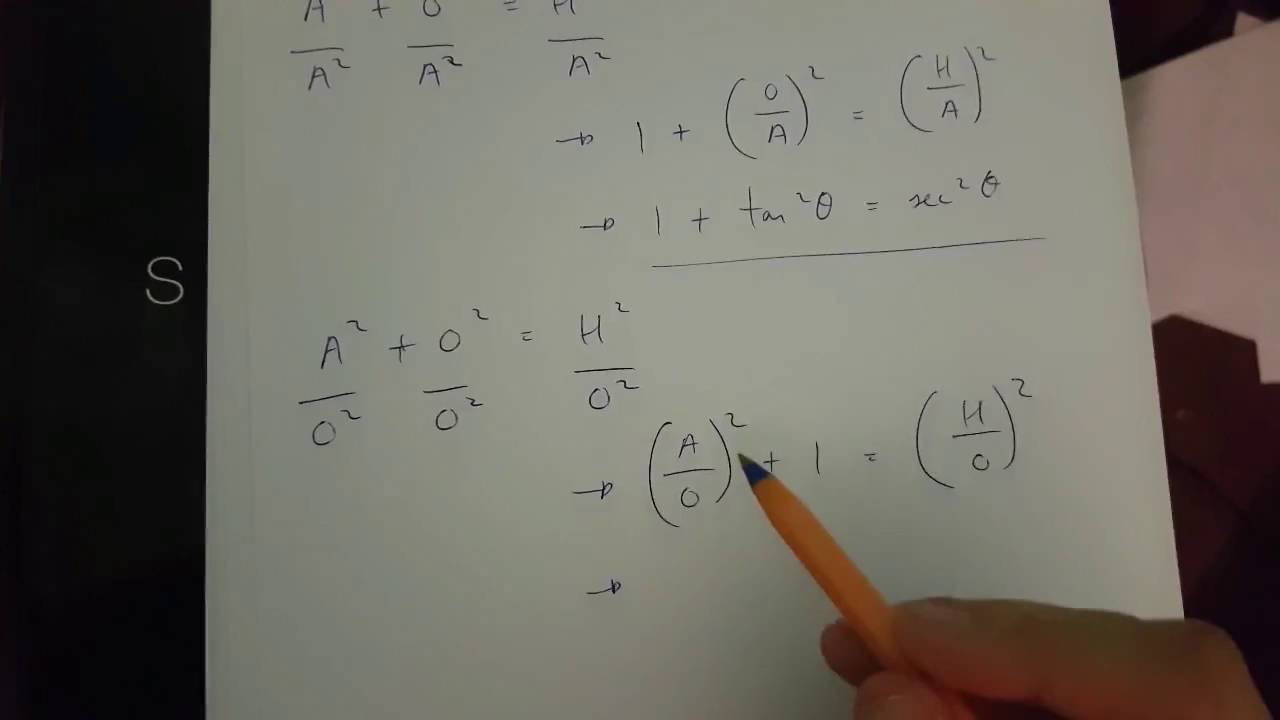



How Do You Prove Tan 2x Secx 1 1 Secx Socratic
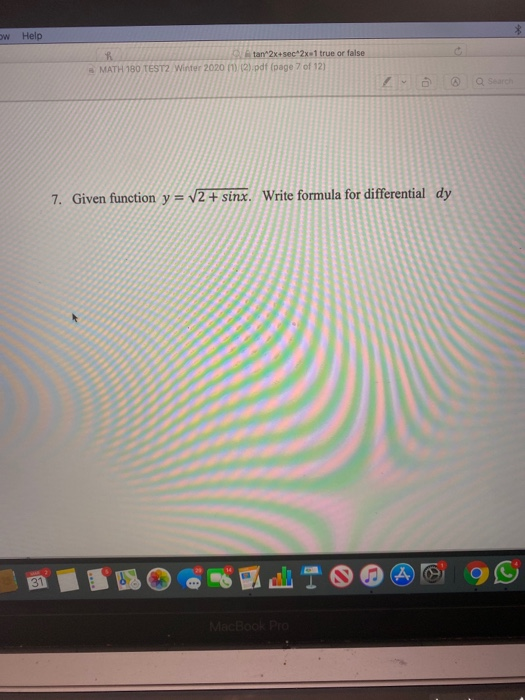



Solved W Help Tan 2x Sec 2x1 True Or False 2 Pdf Page 7 Chegg Com




Fallsem 21 Mat01 Eth Vl Reference Material I 15 Jul Mat01 Se Book Module 1 1 Pages 301 350 Flip Pdf Download Fliphtml5



Dxyot5v7ekyzfm




Solved True False For Trig Identities Sin X Sin X Chegg Com



What Is Math Int Tan 2 2x Dx Math Quora




Tangent Half Angle Formula Wikipedia




Trig Identity Sec2x Minus Tan2x T10 Youtube




Plz Explain Why A If F X Is Continuous On A B Then F X J R L Do S Homeworklib




Derivative Of Tan X Old Video Khan Academy




The Equation Sec 2x 1 Tan 2x Is An Identity True Or False
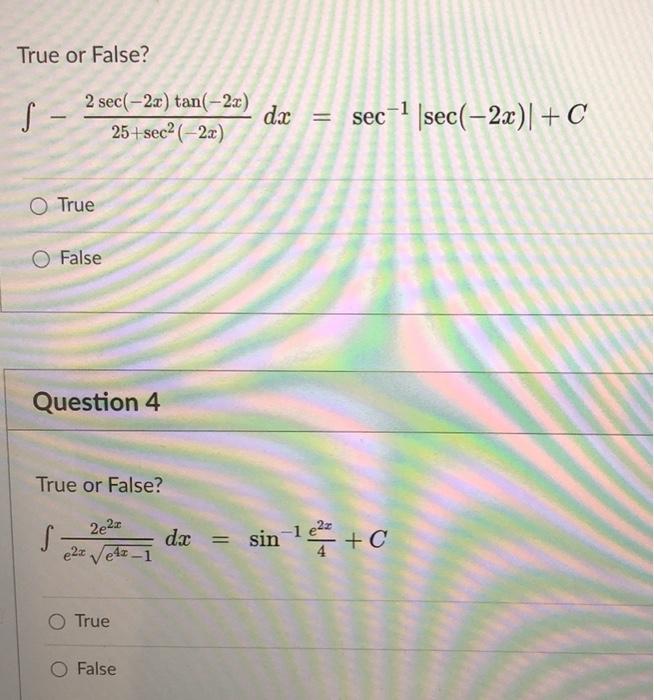



Solved True Or False S 2 Sec 22 Tan 23 25 Sec 2x Dx Chegg Com
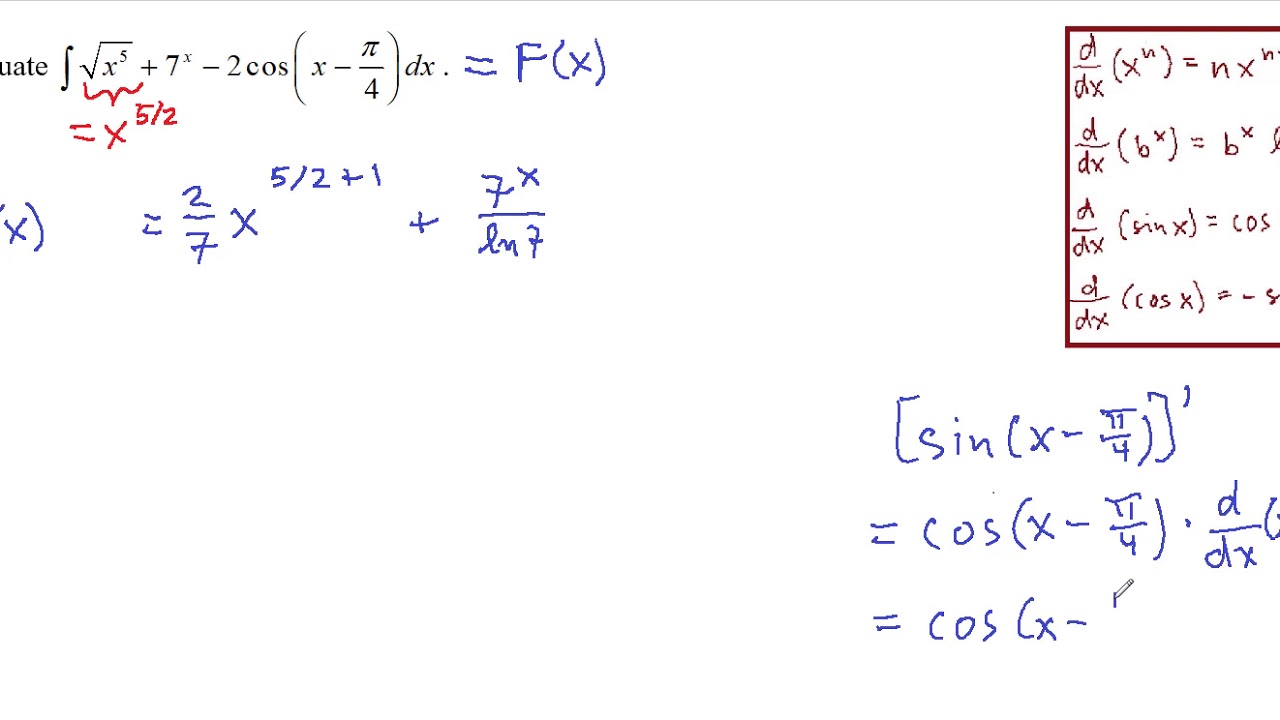



Indefinite Integrals




1 Tan 2x 1 Cos 2x Sin 2x 2sin 4x 1 Sin 2x Trigonometric Identities Mcr3u Youtube




Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo




Solution Integral Of 3 Sec 2x 1 Tan 2x 1 Studypool




Solved Enter T Or F Depending On Whether The Statement Is Chegg Com
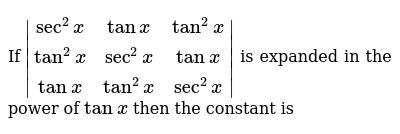



The Equation Sec 2x 1 Tan 2x Is An Identity True Or False
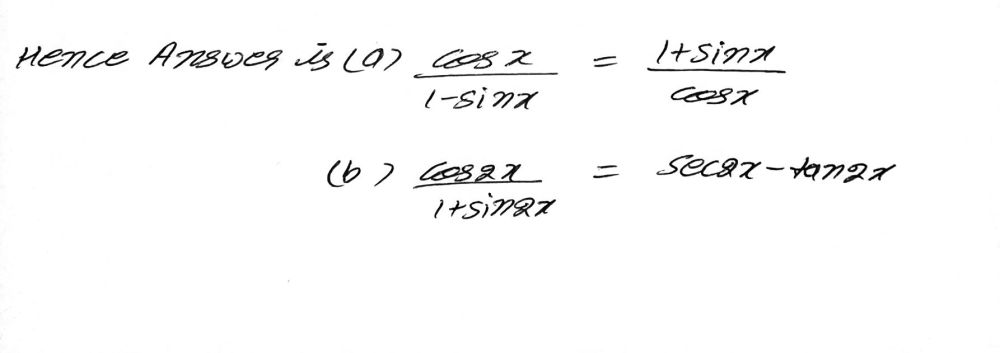



Prove Each The Following Trigonometric Identities Gauthmath



Calculated Formula Questions Blackboard Help
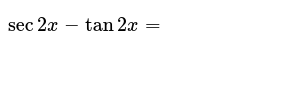



The Equation Sec 2x 1 Tan 2x Is An Identity True Or False




How Do You Verify 4tan 4 Tan 2x 3 Sec 2x 4tan 2x 3 Kinda Hard Please With All The Steps Thanks Socratic



2




Sec 2x1 Cos2 X Tan 2x Tantx 3 Esus Is Always The Ans イais 1 0 If You Are A Student Follow Tumblr Meme On Me Me




Derivative Proofs D Dx Tan X Sec 2 X Youtube



1
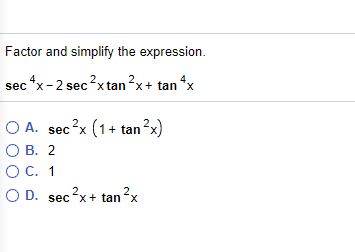



Solved Factor And Simplify The Expression Sec 4 X 2 Chegg Com
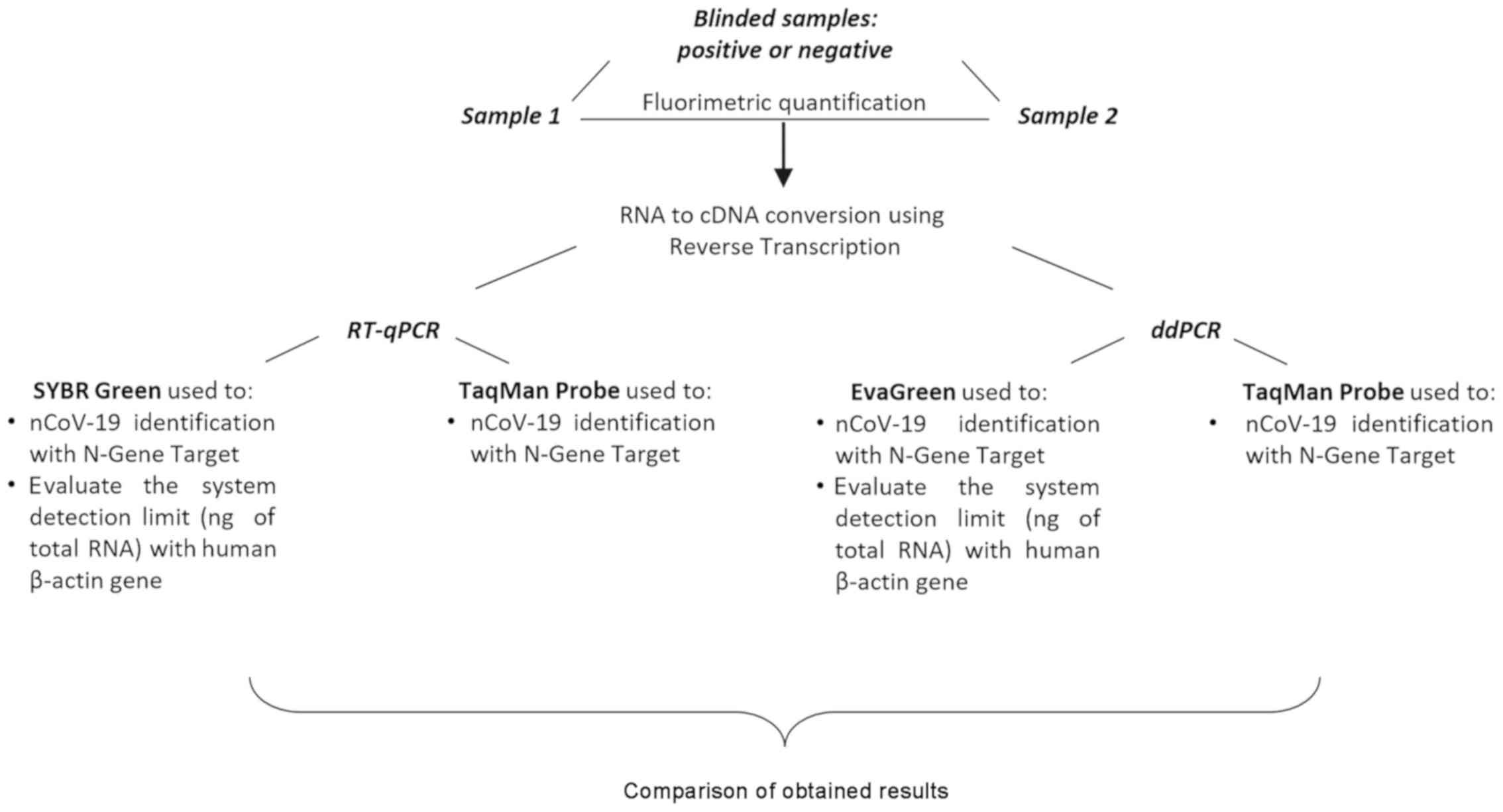



Sensitivity Assessment Of Droplet Digital Pcr For Sars Cov 2 Detection




Question Video Differentiating Functions Involving Trigonometric Ratios Using Pythagorean Identities Nagwa
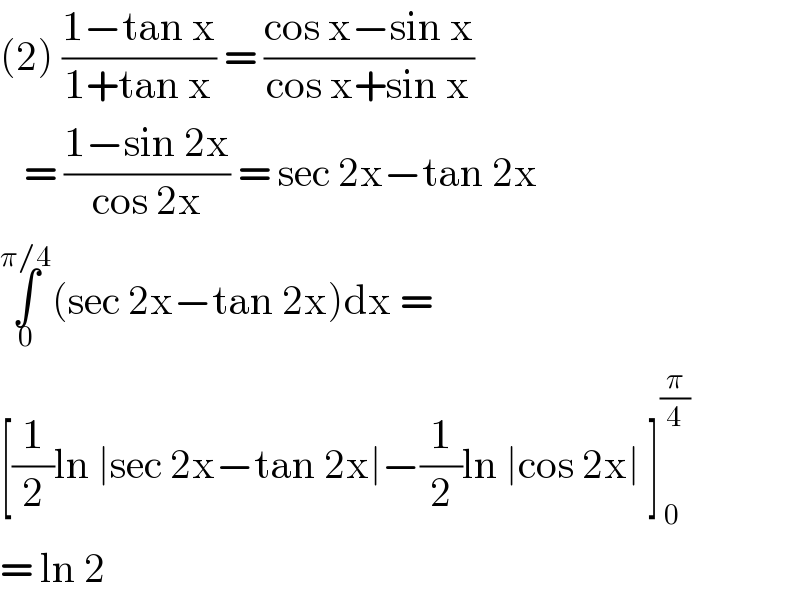



Tinkutara Equation Editor Math Forum Question




Why Is The Graph Of Sec 2 X Tan 2 X Continuous At X Pi 2 Mathematics Stack Exchange



What Is The Integral Of Tanx Sec 2x 1 Tan 2x Quora




I M Seriously Confused About This Trigonometry Problem Askmath



0 件のコメント:
コメントを投稿