F(x)=x^3-1/x^3 find f(x) f(1/x) 276996

Area between y = x^2 and x = 1 and x = 3F (x) = (x1) (x2) (x3) , x ∈ 0,4, ∴ f (x) = x 3 6x 2 11x 6 As f (x) is a polynomial in x (1) f (x) is continuous on 0, 4 (2) f (x) is differentiable on (0, 4) Thus, all the conditions of LMVT are satisfied To verify LMVT we have to find c ∈ (0,4) such thatThe output f (x) is sometimes given an additional name y by y = f (x) The example that comes to mind is the square root function on your calculator The name of the function is \sqrt {\;\;} and we usually write the function as f (x) = \sqrt {x} On my calculator I input x for example by pressing 2 then 5 Then I invoke the function by pressing

More Differentiation By First Principles

F(x)=x^3-1/x^3 find f(x) f(1/x)

F(x)=x^3-1/x^3 find f(x) f(1/x)- If f(x)=3x2,find f^1(x) Get the answers you need, now!Calculus Examples Popular Problems Calculus Find the Critical Points f (x)=x^ (1/3) (x4)

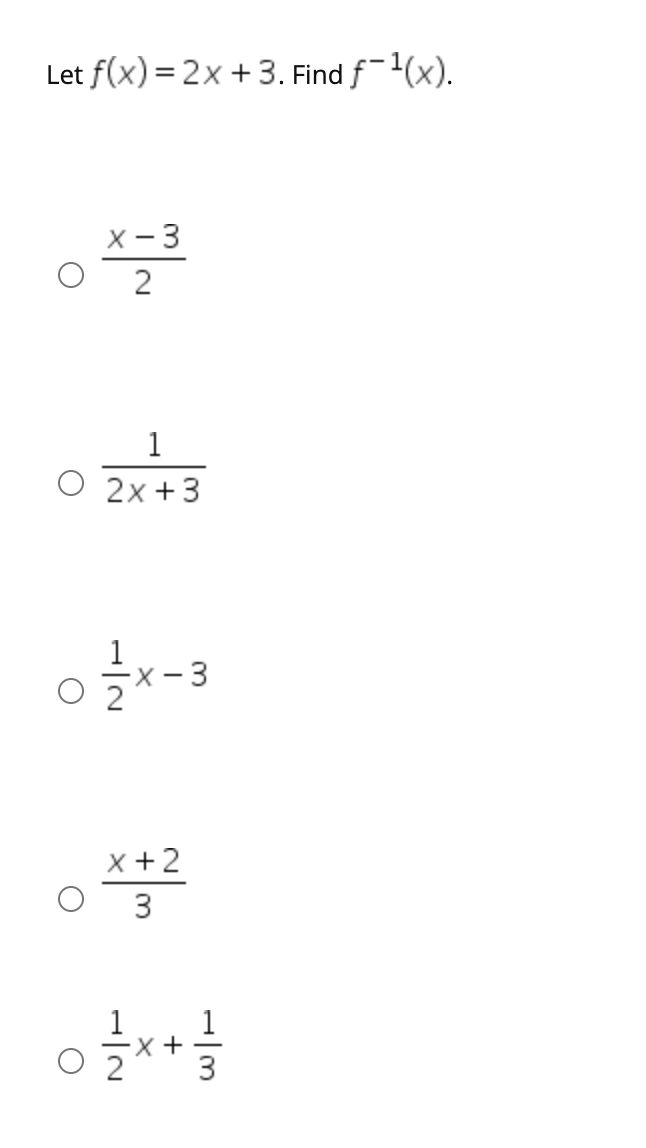
Let F X 2x 3 Find F 1 X X 3 2 1 O 2x 3 O X 3 Chegg Com

Answer to 1 Find f '(x) and f ''(x) f(x) = (x3 5)ex 2 3Mr Dwyer is available for 1on1 tutoring online Details at https//www4tutorcom/onlinetutoringRestated that is f(x)=2x^21 and g(x)=x4 find (fog) (x) Solve the following x log base 2(3x5)=3log2 (3x5)=3 Answer by longjonsilver(2297) ( Show Source )

Related Queries calculate how drenched I would become if I walked in the rain; 36 A function g is described below g(x) = (x 3)2 1 • The domain of g is all real numbers greater than 0 The range of g is all real numbers gre ater than or equal to F 1 H 3 G 3Osculating circle y = 1/x^2 at x = 2;

Find {eq}\displaystyle f'' (1) {/eq}, if {eq}\displaystyle f(x) = 3 x^2 5 x 7 {/eq} Second Derivative The second derivative of the function is the derivative of the first derivative or justSimple and best practice solution for f(x)=(x3)(3x1)(x1) equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve itAlgebra Examples Popular Problems Algebra Find the Inverse Function f (x)=x^31

Solving Polynomial Equations Answers

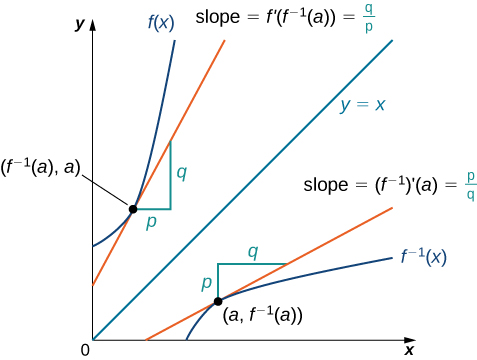
3 7 Derivatives Of Inverse Functions Mathematics Libretexts

Find f'(a) f(x) = x^{2} Video Transcript So for this problem, we're going to be taking the derivative of ffx and then we want to evaluate it at a specific value at this point for this problem is just gonna be the value of a So what we have is ffx is equal to X to the negative, tooGiven f(x) = x^3 3x^2 – 1 Use the first or second derivative tests to a) Find the relative extrema b) Determine the intervals where the graph is increasing or decreasingShort Solution Steps f ( x ) = x ^ { 3 } ( 1 \frac { 4 } { x 6 } ) f ( x) = x 3 ( 1 − x 6 4 ) To add or subtract expressions, expand them to make their denominators the same Multiply 1 times \frac {x6} {x6} To add or subtract expressions, expand them to make their denominators the same

Http Cbsd Org Cms Lib010 Pa Centricity Domain 49 Day 8 section 1 9 inverse functions f16 class notes Pdf

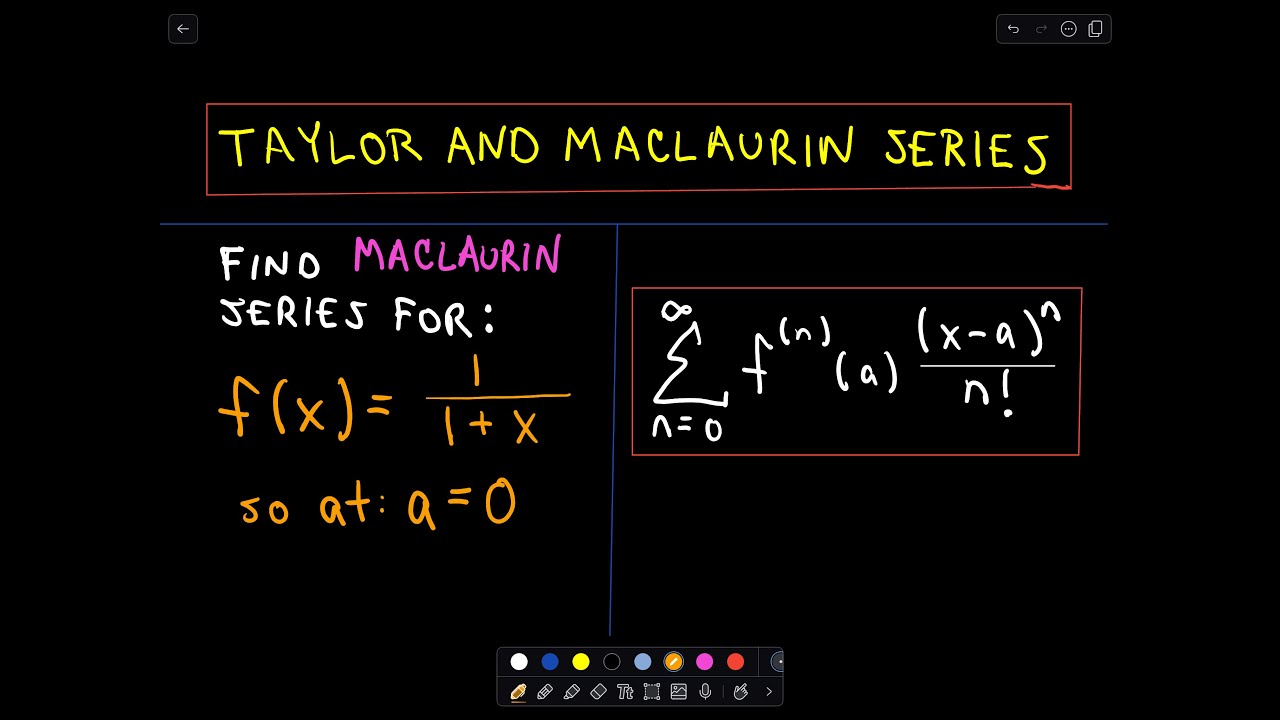
Finding A Maclaurin Series Expansion Another Example 1 Youtube

3 (x 1)2 − 7 View solution steps Solution Steps f ( x ) = 3 ( x 1 ) ^ { 2 } 7 f ( x) = 3 ( x 1) 2 − 7 Use binomial theorem \left (ab\right)^ {2}=a^ {2}2abb^ {2} to expand \left (x1\right)^ {2} Use binomial theorem ( a b) 2 = a 2 2 a b b 2 to expand ( x 1) 2 3\left (x^ {2}2x1\right)7Explanation Using the defined function, f(a) will produce the same result when substituted for x f(a) = a 2 – 5 Setting this equal to 4, you can solve for a a 2 – 5 = 4 a 2 = 9 a = –3 or 3Y=f(x)= x 3 による逆像。 立方根 3 √の定義 ※一般化：べき関数y=x n によ る逆像

Ap Calculus Ab If F X Int 1 X 3 1 1 Ln T Dt X 1 Find F 2 Free Math Help Forum

Answered Nobem 13 G X 1 X 1 Fx 1 X 2 Bartleby

Answer to If f(x) = 3x 7 and g(x) = (x)^{3} 1, then find (f \\circ g)(2) By signing up, you'll get thousands of stepbystep solutions to f(x) = {(3x)/(1x)} 23x taking log on both sides log(fx) = (2 3x) log {(3x)/(1x)} log(fx) = (2 3x) log(3x) log(1x) Now differentiate f'(x) /f(x) = (21 The continuos function f R → R defined by rule f(x) = x5 x3 x is stricly incrasing, then the equation f(x) = 3 has only a single solution But 15 13 1 = 3, then x = 1 is single solution the equation f(x) = 3 therefore f − 1(3) = 1 Clearly f − 1(f(2)) = 2 because f is bijection Share

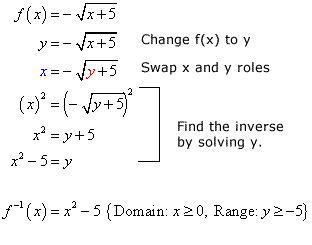
Inverse Of Square Root Function Chilimath

Inverse Functions Differentiation

Understanding function notationNeed more help?ML Aggarwal Solutions for Class 10 Maths Chapter 6 Factorization p = 6/6 p = 1 Therefore, value of p is 1 (ii) Find 'a' if the two polynomials ax3 3x2 – 9 and 2x3 4x a, leaves the same remainder when divided by x 3Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history

2

Inverse Functions And Logarithms Pdf Free Download

X!a f(x) g(x) = 1, If the values of f(x) g(x) are negative as x!ain the above situation, then lim x!a f(x) g(x) = 1 , If on the other hand, if lim x!ag(x) = 0 = lim x!af(x), we cannot make any conclusions about the limit Example Find lim x!ˇ cosx x ˇ As xapproaches ˇfrom the left, cosxapproaches a nite number 1 As xapproaches ˇfrom theFor example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1 / f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domainCorrect answer \displaystyle 35 Explanation To get each member of this sequence, add a number that increases by one with each element \displaystyle 7 1 = 8 \displaystyle = 10 \displaystyle 103= 13 \displaystyle 134=17

Consider F R 4 3 R 4 3 Given By F X 4x 3 3x 4 Show That F Is Bijective Find The Inverse Of F And Hence Find F 1 0

2 Inverse Functions Limits Involving Infinity Asymptotes Of Graphs Studocu

F (x) = (x3)/ (x1) Let f (x) = u/v such that\ u= x3 ==> u' = 1 v= x1 ==> v'= 1 f' (x) = (u'v uv')/v^2 = 1* (x1) (x3)*1/ (x1)^2 = (x1 x 3)/ (x1)^2 = 4/ (x1)^2 f' (0) = 4F(x3) = 5x2 f(x3) = 5(x3)13 That is f(x) = 5x13 or f(x3) = 5x2 put x = x3 f(x33) =5(x3)2 f(x) = 5x152 f(x) = 5x13Answer to If f(x) x2f(x)3 = 10 and f(1) = 2, find f '(1)f '(1) =

If F X 3 X 1 X 2 3x Find F 0 Maths Continuity And Differentiability Meritnation Com

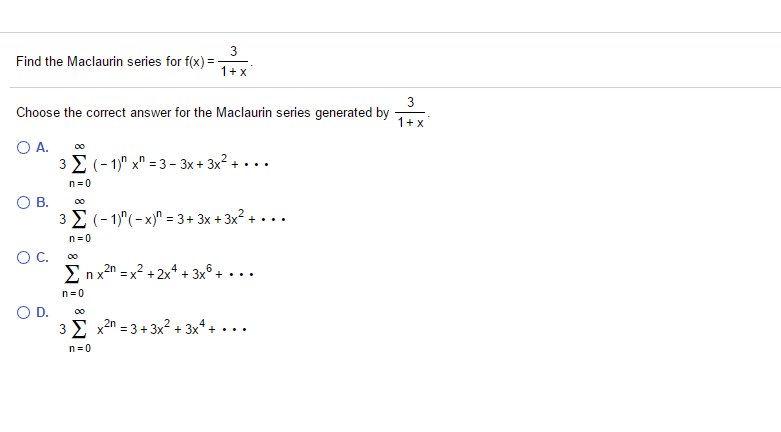
Find The Maclaurin Series For F X 3 1 X Choose Chegg Com

 1 Answer Monzur R In order to find for any function f (x), we must apply the 'transformation' y = x In order to do that, we must define x in terms of y, ie, find f (y), then set y = x Let y = f (x) y = (x − 3)3 1 y − 1 = (x −3)3 x − 3 = 3√y − 1Solution for f (x)=x^31 equation Simplifying f (x) = x 3 1 Multiply f * x fx = x 3 1 Reorder the terms fx = 1 x 3 Solving fx = 1 x 3 Solving for variable 'f' Move all terms containing f to the left, all other terms to the right Divide each side by 'x' f = 1x 1 x 2 Simplifying f = 1x 1 x 2G(x) = tanh(2x) gives f(x) = (1 x4) 128x4 Not a polynomial, but at least a rational function g(x) = tanh(3 2x) gives f(x) = 1 x3 which is the answer given by juantheron For RHS to be a polynomial you have a0 = 1 or a0 ≠ 1 and ai = 0 for i > 0 (which contradicts an ≠ 0 )

Linear Approximations And Differentials

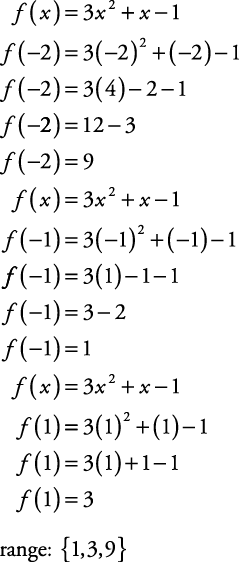
Functions

Q Evaluate lim f(x) and lim f(x) for the following function Then give the horizontal asymptote of f ( Then give the horizontal asymptote of f ( A Click to see the answerMathf(x1)=2x3/math Let matht=x1\implies x=t1/math math\therefore f(t)=2(t1)3/math mathf(t)=2t5/math matht/math can be replaced by mathx1 Example 1 f(x) = x We'll find the derivative of the function f(x) = x1 To do this we will use the formula f (x) = lim f(x 0 0) Δx→0 Δx Graphically, we will be finding the slope of the tangent line at at an arbitrary point (x 0, 1 x 1 0) on the graph of y = x (The graph of y = x 1 is a hyperbola in the same way that the graph of

If X 1 X 3 Then What Is The Value Of X 1 X Quora

Find Equation Of Tangent To Y X 3 1 X 2 Find Interval Where

Let f be a real valued function defined on the interval (− 1, 1) such that e − x f ( x ) = 2 ∫ x t 2 1 d t , ∀ x ∈ ( − 1 , 1 ) and let f − 1 be the inverse function of fIf f (x) = x1/x1 then find the value of f (2x) Find the answer to this question along with unlimited Maths questions and prepare better for JEE examination> 1 Taylor polynomials > 11 The Taylor polynomial Example Find a quadratic polynomial p 2(x) to approximate f(x) near x= a Since p 2(x) = b 0 b 1xb 2x2 we impose three conditions on p 2(x) to determine the coefficientsTo better mimic f(x) at x= awe require

3 13 Points Let F X X X 3 1 You Are Given Chegg Com

Example 1 Find An Inverse Relation Find An Equation For The Inverse Of The Relation Y 3x 5 Write Original Relation Y 3x 5 Switch X And Y X Ppt Download

 Ex 13, 3Find 𝑔𝑜𝑓 and 𝑓𝑜𝑔, if(i) f(x) = 𝑥 and g (x) = 5𝑥 −2f(x) = 𝑥 , g(x) = 5𝑥−2f(x) = 𝑥f(g(x)) = 𝑔(𝑥)fog(x) = (5𝑥 −2) = 𝟓𝒙 −𝟐g(x) = 5𝑥 −2g(f(x)) =5𝑓(𝑥) −2gof (x) = (𝟓𝒙−𝟐) Misc 7 Find intervals f(x) = x3 1/x3 x = 0 is increasing Misc 7 Find the intervals in which the function f given by f (x) = x3 1/𝑥^3 , 𝑥 ≠ 0 is (i) increasing (ii) decreasingf(𝑥) = 𝑥3 1/𝑥3Finding f'(𝒙) f'(𝑥) = 𝑑/𝑑𝑥 (𝑥^3𝑥^(−3) )^ = 3𝑥2 (−3)^(−3 − 1)= 3𝑥2 – 3𝑥^(−4)= 3𝑥^2−3/𝑥^4 = 3(𝑥^2−1/𝑥^4Use Descartes' Rule of Signs to find the number of real roots off (x) = x5 4x4 – 3x2 x – 6 First, I look at the positiveroot case, which is looking at f (x) f ( x) = x5 4 x4 – 3 x2 x – 6 The signs flip three times, so there are three positive roots, or one positive root Either way, I definitely have at least one positive

Mcq Class 12 If F X 3 X 3 1 3 Then Fof X Is Teachoo

If X 1 X 3 Then What Is The Value Of X 1 X Quora

1 f X(y 1 n) where, f X() is the pdf of X which is given Here are some more examples Example 1 Suppose Xfollows the exponential distribution with = 1 If Y = p X nd the pdf of Y Example 2 Let X ˘N(0;1) If Y = eX nd the pdf of Y Note Y it is said to have a lognormal distribution Example 3 Let Xbe a continuous random variable with pdf fInverse\f (x)=\frac {1} {x^2} inverse\y=\frac {x} {x^26x8} inverse\f (x)=\sqrt {x3} inverse\f (x)=\cos (2x5) inverse\f (x)=\sin (3x) functioninversecalculator enThen I'll make it simpler for us in the long run, that tells us that F prime of X is going to be X to the negative one over a negative one, which is just negative one over Acts plus C That tells us that F of X is going to be equal to negative the anti derivative of one over X is actually going to be the natural log of the absolute value of X

Example 4 Show F X X3 3 1 Is Not Continuous At X 0

If F R To R Be A Function Defined As F X 3 X 3 1 3 Find F X Brainly In

Find (f B g)(3) and (g B f)(3) if f ( x ) = x 2 and g ( x ) = 4 – x2 Solution Step 1 Find (f B g)(x) then evaluate for 3 Since (f B g)(x) = f( g(x) ), then = f(4 – x2) = (4 – x 2) 2 = 6 – x 2 Evaluating for 3 (f B g)(3) = 6 – (3)2 = 6 – 9 = 3 0DWK 6WXGHQW /HDUQLQJ $VVLVWDQFH &HQWHU 6DQ $QWRQLR &ROOHJHF (x)= 1−x3 −x5The critical point of F (x) are the values of xfor which either f ′(x) does not exist or f ′(x)= 0So f (x)= 1−x3 −x5f ′(x) = −3x2 −5x4f ′(x) = 0 when x = 0x = 0 is the only critical point because 35x2 > 0for all x ∈ Rf is decreasing on all the x value (x ∈ R)because f ′(x) < 0 for all xOne class collects 8 1/4 pounds of recyclable materials Another class collects 1 1/2 times as many pounds as the first class

Horizontal Line Test For Function To Have Inverse Expii

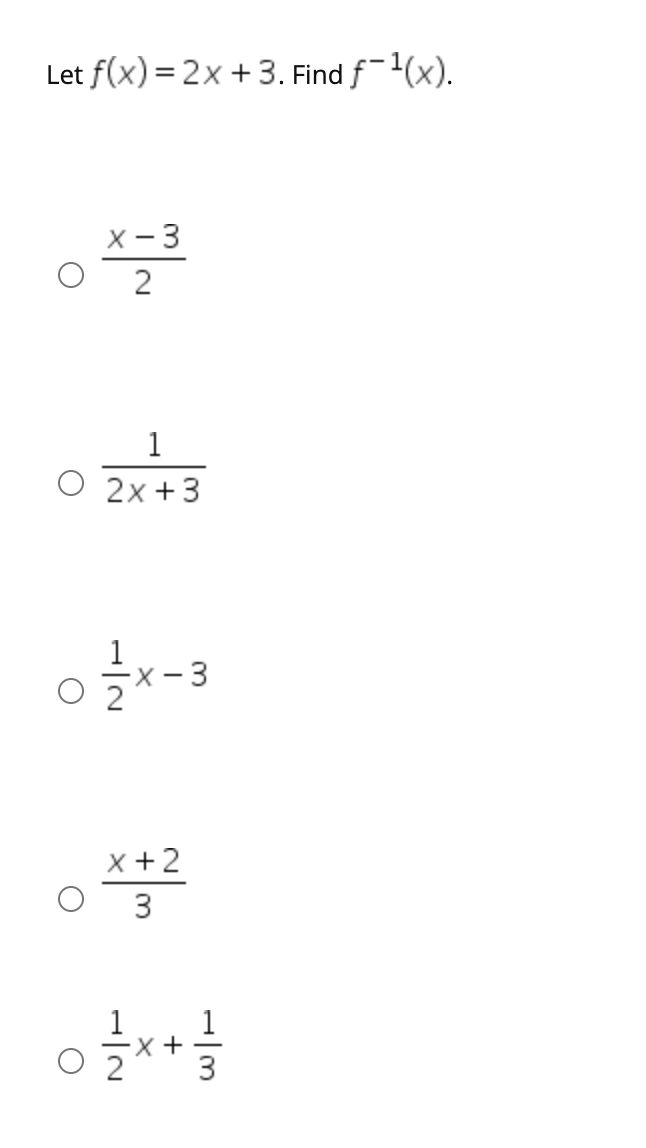
Let F X 2x 3 Find F 1 X X 3 2 1 O 2x 3 O X 3 Chegg Com

Www Math Uh Edu Jiwenhe Math1432 Lectures Lecture01 Handout Pdf

Is G 1 1 2 3 3 5 4 7 A Function If This Is Described By The Formula G X Alpha X Beta Then What Values Should Be Assigned To Alpha And Beta

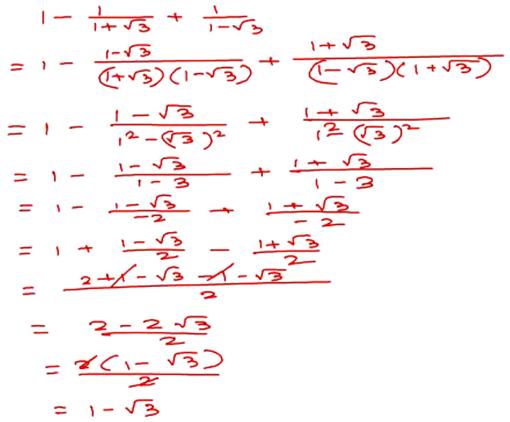
Free Math Answers Answers Within 24 Hours Step By Step Explanations

Find

Find The Inverse Of The One To One Function 7 3x 1 Chegg Com

Find The Intervals In Which The Function F Given By F X X 3 1 X 3 X 0 Is Mathematics Shaalaa Com

Math Scene Equations Iii Lesson 3 Quadratic Equations

Answered Let F X 2 X And G X 1 X Bartleby

If A Function F R R Be Defined By F X 3x 2 X 0 1 X 0 4x 1 X 0 Find F 10 F 1 F 0 F 2 Dot

More Differentiation By First Principles

If F R R Is Defined By F X X 3 Then F 1 8

Math Scene Equations Iii Lesson 3 Quadratic Equations

Functions Algebra Mathematics A Level Revision

If The Function F R To R Be Given By F X X 2 And G R To R Be Given By G X X X 1 X Not Equal To 1 Find Fog

He Functions Fand G Are Defined By Fx X 3 1 And Gauthmath

7 1 Operations On Functions Operationdefinition Ppt Download

Faculty Math Illinois Edu Pat Fa07 Lab Pracmast2sol Pdf

1 Evaluate The Following F X X2 1 And G X 3x 5 16 Points A S 3 B G 2 Homeworklib

Let F X 1 X 0 X 2 3 X 2 Lt X Lt 3 Determine The Form Of Brainly In

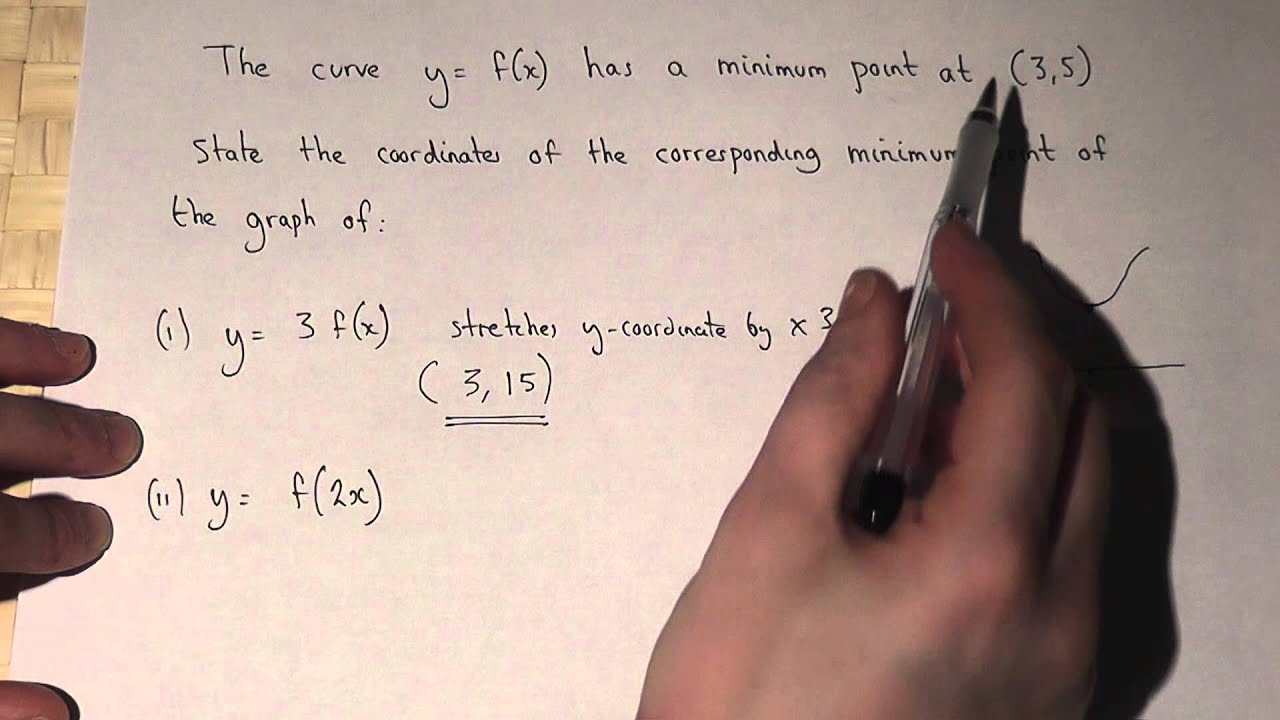
Graph Transformations Y 3f X And Y F 2x Youtube

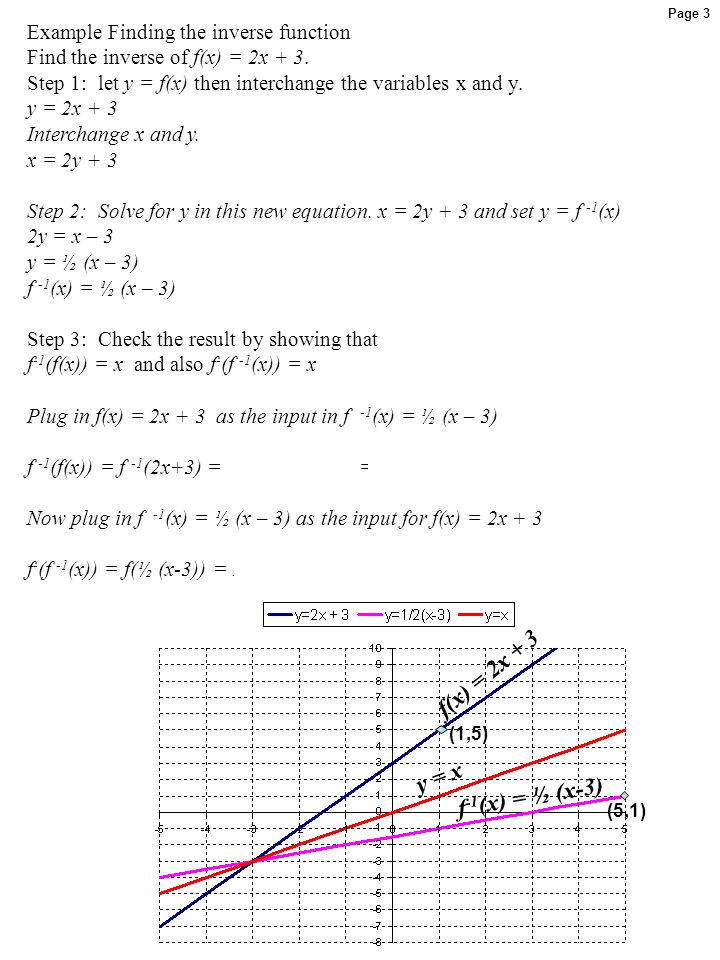
Function F Function F 1 Ch 9 4 Inverse Functions Ppt Download

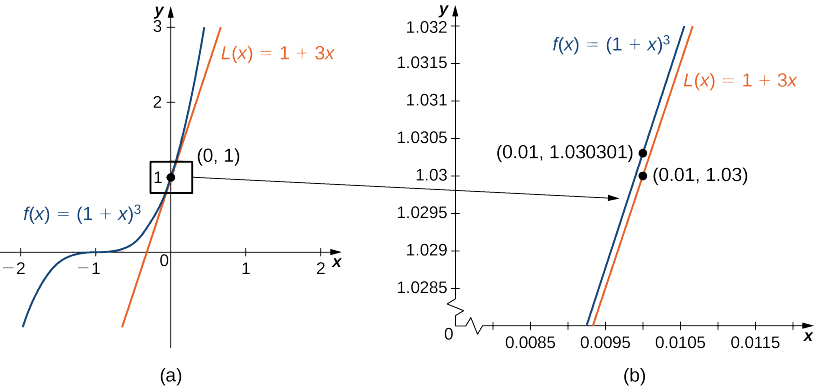
4 2 Linear Approximations And Differentials Mathematics Libretexts

Domain And Range Of F X X 3 X 3 Are Respectively

Composition Of Functions Composing Functions At Points

Http Www Math Umd Edu Immortal Math115 Sect2 78 Ln Pdf

Rd Sharma Solutions For Class 11 Maths Updated For 21 22 Chapter 3 Functions

Q Tbn And9gcr8gxoxnnv44em49b8rhzmoidze2bkxol Lomadtp4qe2fejvyf Usqp Cau

Implicit Differentiation

Wolfram Alpha Examples Step By Step Solutions

Q Tbn And9gctyxe8grt1m3ttrvwfywcpshoznwmezq2koqwgv1j6bpk7jokud Usqp Cau

Math Scene Equations Iii Lesson 3 Quadratic Equations

If X 1 X 3 Then What Will Be The Value Of X Quora

Ppt 7 5 Inverse Function Powerpoint Presentation Free Download Id

Free Math Answers Answers Within 24 Hours Step By Step Explanations

Qno32 Fx X 3 1 X 3 Show That Fx F 1 X 0 29 Function F R Be By Find F L F 00 If F X Find Maths Relations And Functions Meritnation Com

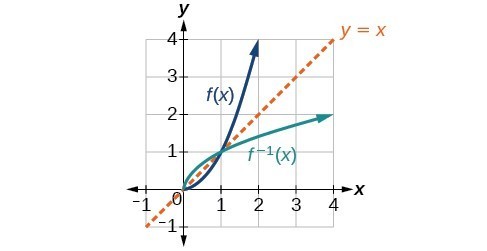
Use The Graph Of A Function To Graph Its Inverse College Algebra

Let F X 1 X 0 X 2 F X 3 X 2 X 3 Determine The Form Of G X F F X And Hence Find

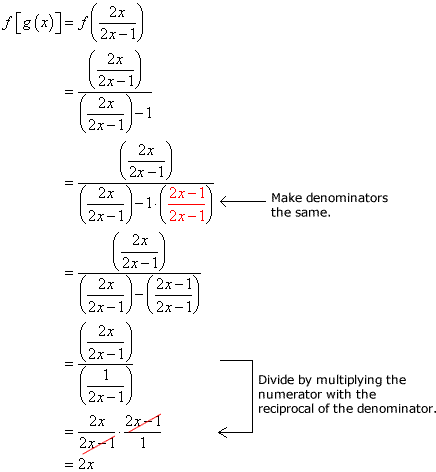
Verifying If Two Functions Are Inverses Of Each Other Chilimath

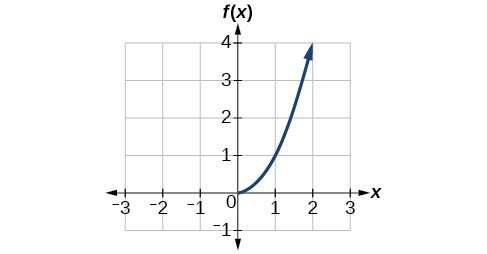
Use The Graph Of A Function To Graph Its Inverse College Algebra

Com Converted Flip Ebook Pages 1 3 Anyflip Anyflip

Inverse Functions Differentiation

Www Math Utah Edu Wortman 1050 Text If Pdf

If F X 2x 3 G X X 3 5 Then Find Fog And Show That Fog Is

If F X X3 1 X3 Prove That F X F 1 X 0 Maths Relations And Functions Meritnation Com

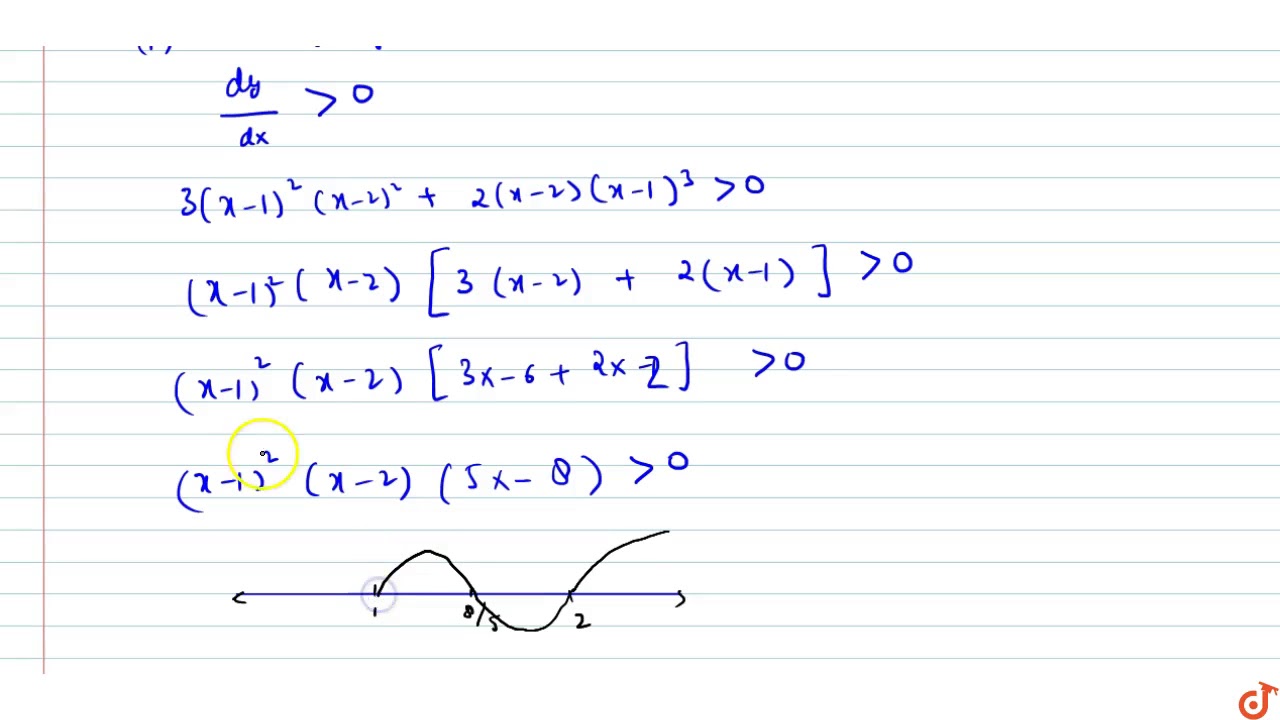
Find The Intervals In Which F X X 1 3 X 2 2 Is Increasing Or Decreasing Youtube

If F X 3 1 X Then F X F Y F Z Is Equal To

Inverse Functions

Section 2 7 One To One Functions And Their Inverses Pdf Free Download

Misc 7 Find Intervals F X X3 1 X3 X 0 Is Increasing

Step By Step Solutions

Q Tbn And9gcqv 2vmvr1v Qsj 8mjzvlnt6dsm1rhps87tautgzqzqa5xgn87 Usqp Cau

1 Let A 2 3 And F X Xx 4x 7 Show That F A 0 Use This Result To Find aaa 1 2 Mathematics Topperlearning Com Dgp2odll

Solve The Problem 23 Given That Fx 3 Finand Give Chegg Com

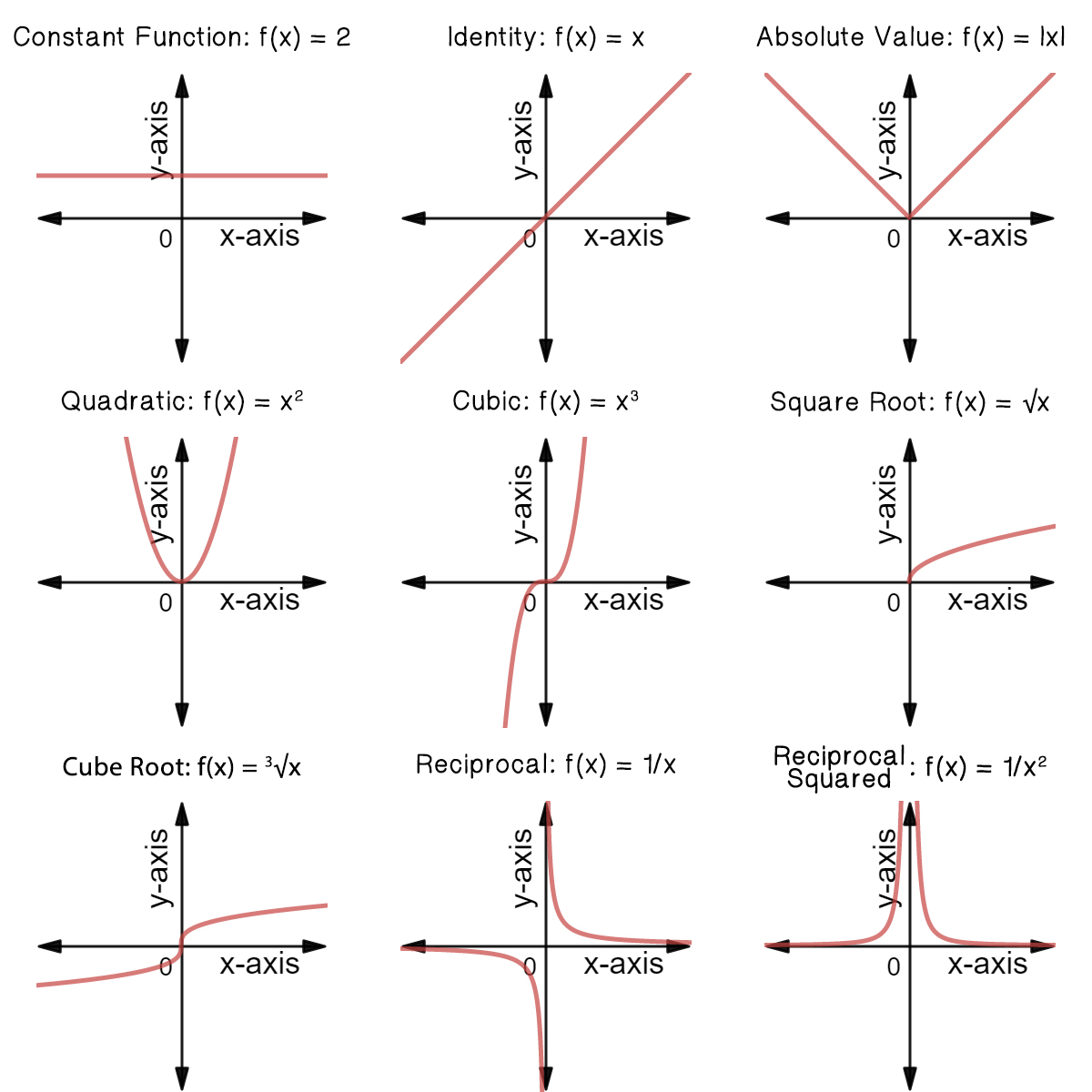
Classifying Common Functions Expii

Solve This Q Find The Intervals In Which The Function F X 3 Log 1 X Maths Application Of Derivatives Meritnation Com

Even And Odd Functions Equations Video Khan Academy

Www Lcps Org Cms Lib Va Centricity Domain 619 Ma calc 3 1 3 2 hmwk Pdf

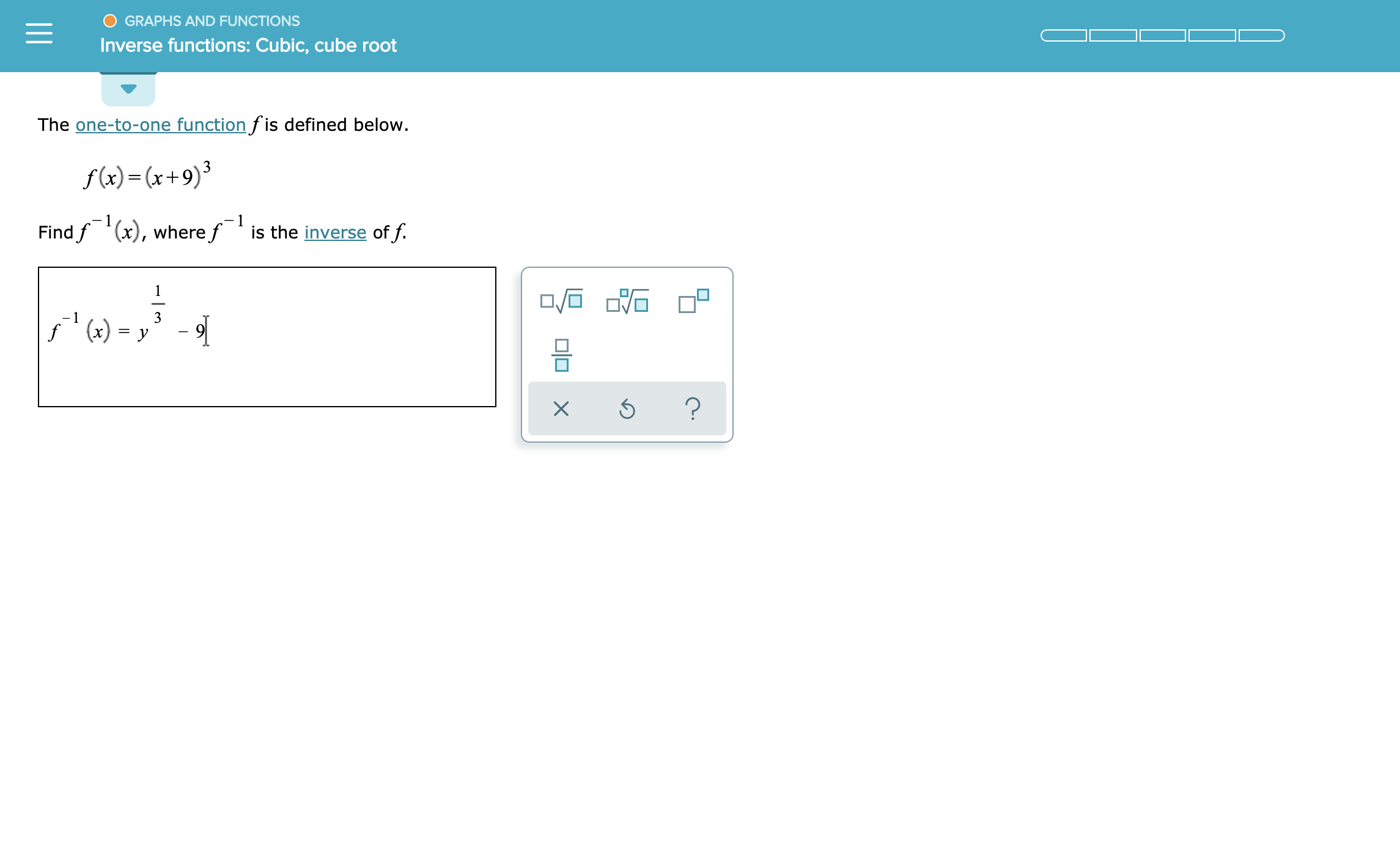
Answered Graphs And Functions Inverse Functions Bartleby

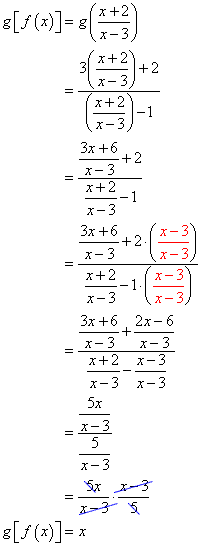
Verifying If Two Functions Are Inverses Of Each Other Chilimath

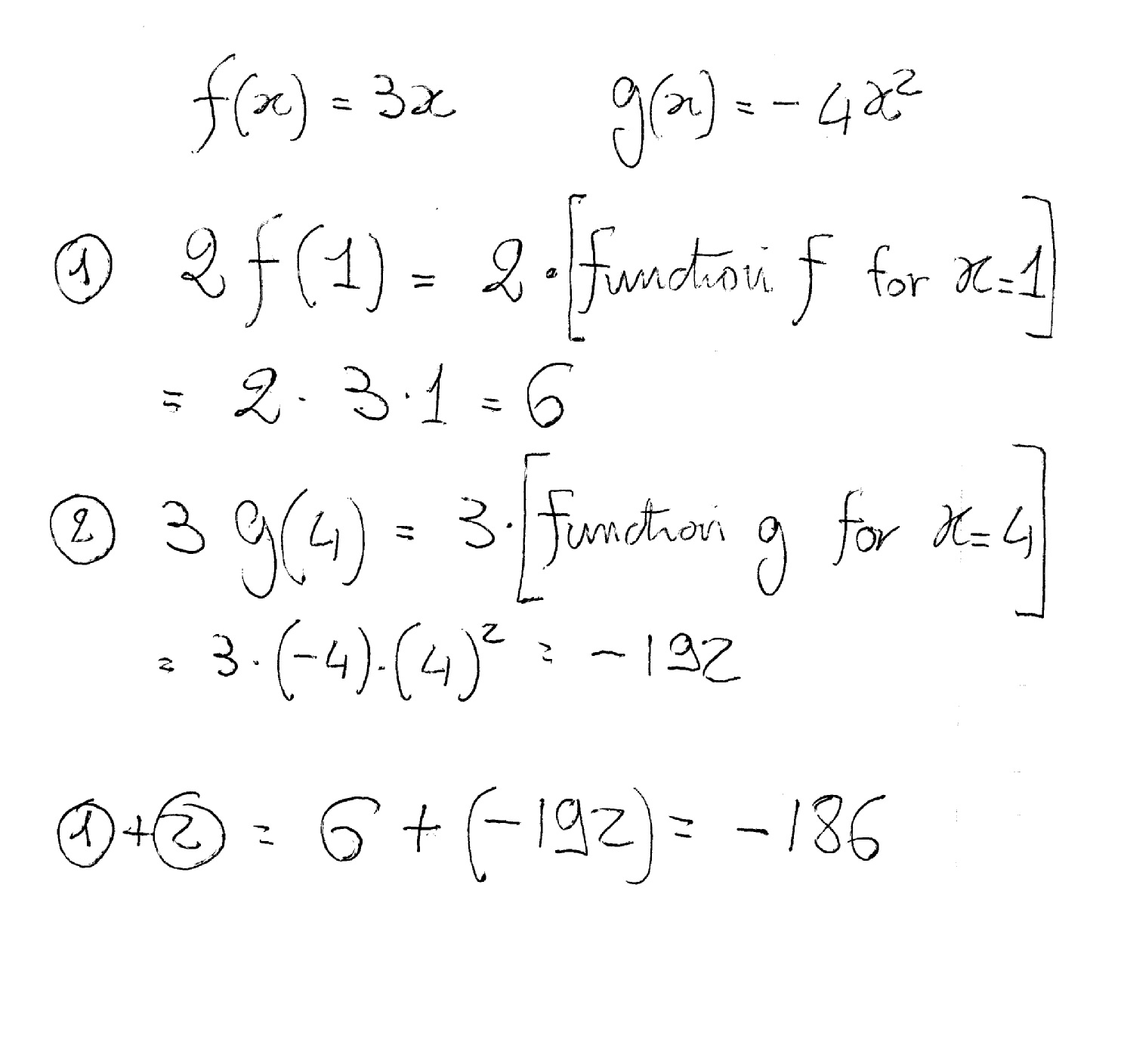
How Do Find The Value Of 2f 1 3g 4 If F X 3x And G X 4x 2 Socratic

Madasmaths Com Archive Maths Booklets Standard Topics Various Function Exam Questions Pdf

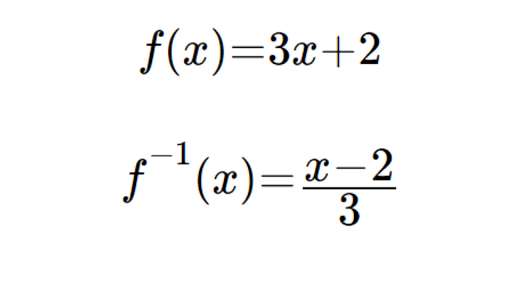
Finding Inverse Functions Article Khan Academy

Excrcises 1

Http Www Math Umd Edu Tvp 460 E2practsol Pdf

Inverse Functions And Logarithms Pdf Free Download

Find The Divided Differences Of 𝑓 𝑥 𝑥3 𝑥 2 For The Argument 1 3 6 11 Wegglab

If F X X 3 1 X 3 Then Find The Value Of F X F X

Derivatives Outcomes Ppt Download

How Do You Find The Derivative Of 3 X 1 Socratic

If X 1 X 3 Then What Is The Value Of X 1 X Quora

Algebra 2 Section 5 3

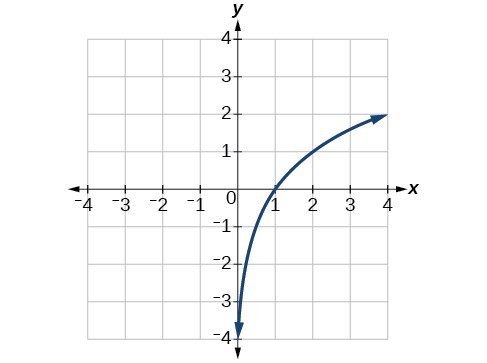
Use The Graph Of A Function To Graph Its Inverse College Algebra

1

Find Domain And Range Of The Functions F X Sin 1 5x F X 1 X 2 X 3 1 X 2 F X Sinx X 2 5x 6 F X Log

Misc 7 Let F X X 1 G X 2x 3 Find F G F G F G

Probability Density Function

Www Math Uh Edu Jiwenhe Math1432 Lectures Lecture01 Handout Pdf

Evaluate Each Function K A 2a 3 1 Find K 3 G X 4 2x 1 7 Find G 1 F X 8x 2 Brainly Com